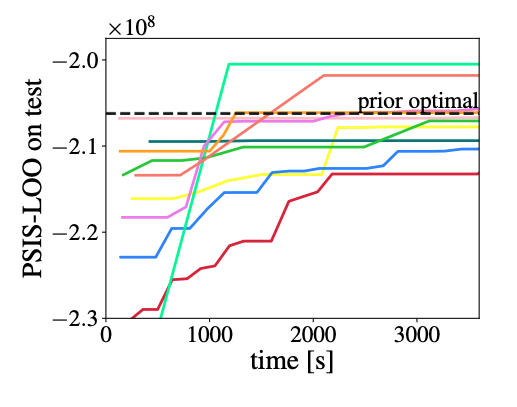
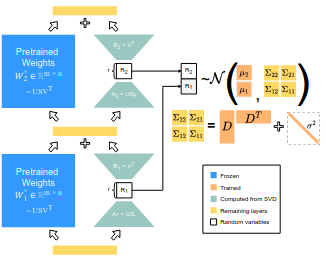
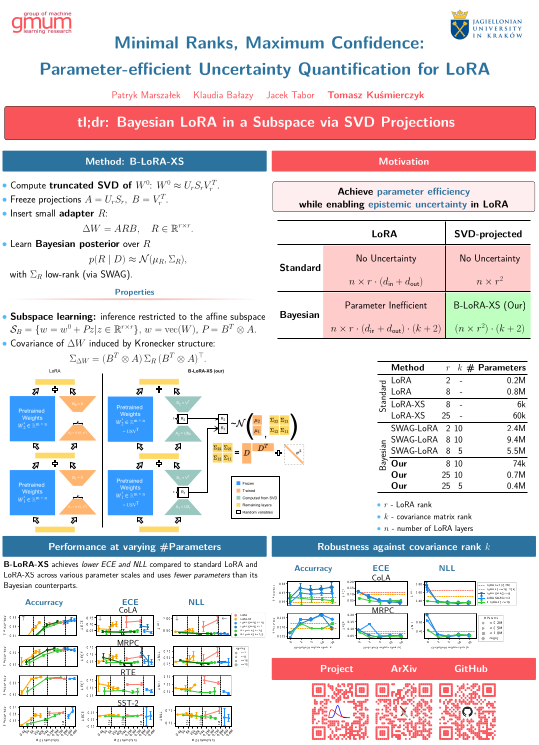
We are recruiting!
We invite you to join our team at the Jagiellonian University in Krakow and contribute to advancements in Bayesian Neural Networks. If you are passionate about Bayesian Deep Learning and want to make a difference, please email us! We offer scholarships for students and doctoral candidates in Poland. The scholarship amounts up to PLN 5000 (approximately EUR 1250), raising the total doctoral student remuneration to PLN 8460 (gross) / PLN 8000 (net) (approximately EUR 2000 gross / EUR 1900 net). This attractive offer is particularly appealing given the affordable living costs in Poland.
A successful candidate will work in the field of Bayesian Deep Learning on a project funded by the National Science Center (European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement) titled Balancing Priors and Learning Biases to Improve Bayesian Neural Networks. The research will be conducted within the Group of Machine Learning Research at the Jagiellonian University. Your role will involve theoretical investigations, model implementation, and experiments focusing on learning and priors for Bayesian Neural Networks. Key topics include uncertainty quantification, priors and posteriors, amortized and boosted posterior models, and deep networks architectures.
Please attach the following documents to your e-mail:
- CV/Resume
- Motivation or cover letter explaining how you can contribute to the project
- Any relevant links or materials demonstrating your skills and knowledge
News
-
-
July 22-26, 2024: Vienna, Austria
Meet us at ICML 2024 in Vienna!
-
-
April 01, 2024: Cracow, Poland
We are excited to announce start of the project!
About
- Title: Balancing priors and learning biases to improve Bayesian Neural Networks
- Acronym: PLBNN
- Principal Investigator: Tomasz Kuśmierczyk, Ph.D.
- Mentor: prof. Jacek Tabor, D.Sc.
Hosting Entity: WMII @ UJ
The project is being executed at the
Faculty of Mathematics and Computer Science of the
Jagiellonian University in Cracow.
Description for the general public
Deep Neural Networks (DNNs) are nowadays the most popular approach used in most applications of AI. They are structures composed of many complex processing layers (hence "deep"), each of which is composed of multiple processing units, so-called neurons (hence "neural").
DNNs are used for making predictions, classifying objects, controlling robots, and many more tasks. They can be viewed as processing machines that when served an input produce relevant outputs. These inputs can be some features, for example, an image of a cat, and outputs can be labels, for example, "cat". The predictions standard DNNs produce are, however, far from perfect and they can be catastrophically incorrect. Being incorrect itself is not such a major issue, but what is important, DNNs do not know when they are incorrect. This is because DNNs do not manage uncertainty well - they are overly confident about their predictions, for example, in the case when they are shown an input that was not previously (during training of such a network) seen.
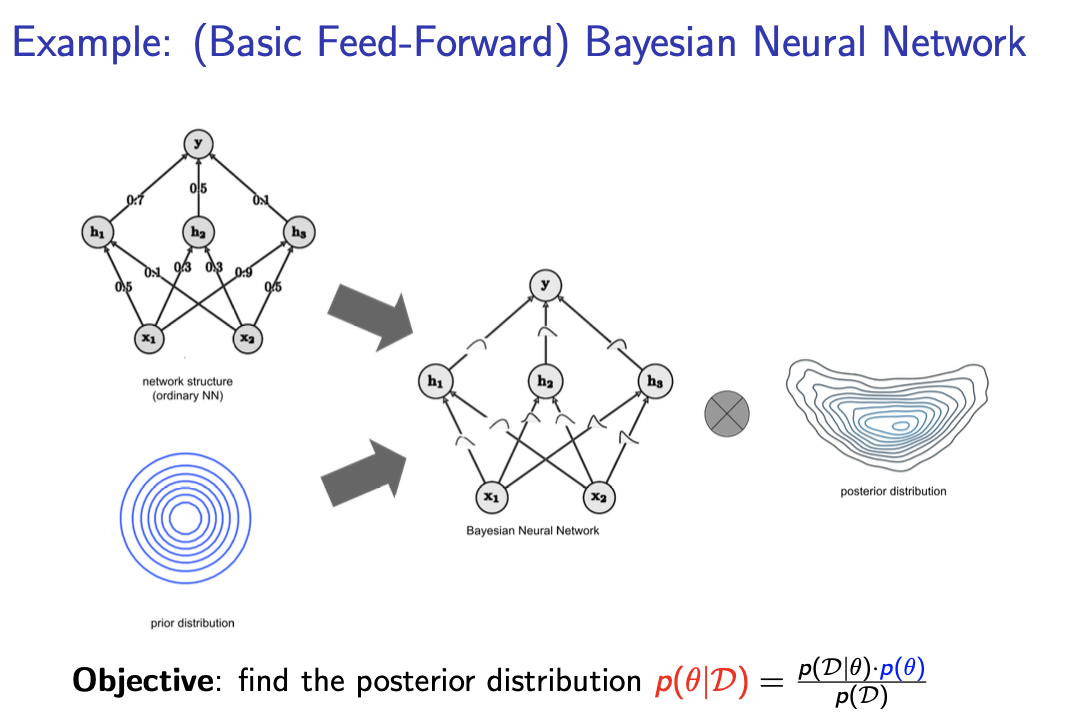
A more reliable counterpart of DNNs is Bayesian Neural Networks (BNNs). BNNs are DNNs in the sense that they follow the same design pattern: consist of multiple complex processing layers. On the other hand, they learn and perform predictions differently, and what is the most important they know when they do not know. This is thanks to the Bayesian inference framework. All information (including predictions) in the Bayesian framework is inherently encoded in a way including information about uncertainty, by representing it with distributions over possible values. It applies also to BNN's parameters: when training a BNN we learn their values only up to some level of certainty.
In Bayesian learning, model before seeing any data is already assumed to encode certain a priori knowledge. In particular, by priors we mean distributions over a model's (e.g. BNN's) parameters (sometimes also over model structure) before actual training or inference is performed. Then, when data is presented to the model it can update these distributions accordingly to the so-called posteriors. For example, before seeing ever a cat we can know it has four legs and a tail, but after seeing some pictures a cat detection model can update itself in a way that it would also check for fur and pointy ears. Nevertheless, if the original beliefs were completely wrong, it would take a long time to adjust them appropriately. Additionally, if they were also too strong it may be entirely impossible.
As illustrated above, setting the priors right is an important part of the model building process. However, for complex models such as BNNs, it is also a nontrivial task, since we lack the intuition about how a particular parameter's value translates to beliefs expressed by model outputs. Furthermore, the previous evidence shows that setting them naively may have significant consequences on performance of the model.
Another problem with BNNs is that finding the posteriors is also a challenging task. This is due to the large number of parameters these models have as well as due to the large size of the data used for training them (=finding posteriors). In practice, posteriors are found only in an approximate way, which often results in suboptimal performance and additionally complicates the understanding of priors' impact.
These limitations taken altogether cause BNNs to perform far below the expectations and the standard DNNs are still used more often in practice.
Our goal is to address some of the above challenges and make BNNs more competitive and release some of their potential. We hypothesize that to achieve better performance for various tasks, network structure, learning approach and priors need to be decided jointly. In particular, priors need to be given more attention and we plan to investigate how better priors can improve the performance of BNNs. Our goal is to make these priors smarter so they would adapt themselves to a given task. This implies two questions: First, how to create such smart and flexible enough priors. Second, how to make them learn with the approximate methods, in a way that BNNs would be competitive in terms of both training time and effectiveness.
To sum up our objectives in this project, we will start by investigating how priors learning can improve the performance of BNNs and when it is optimal to learn priors. We will begin with the identification of selection and learning methods for priors in Bayesian neural networks optimal for various objectives. Furthermore, we will search for optimal architectures of flexible priors and posteriors for parameters of BNNs. We plan to look into structured, hierarchical, and heterogeneous priors. Finally, from a theoretical point of view, we will study the correspondence of the BNNs and other Bayesian models and in particular, how BNNs relate to so-called Gaussian Processes.
We will evaluate our approaches on the standard benchmarks for several interesting and important settings. We aim at improving effectiveness against state-of-the-art approaches for uncertainty quantification.
Funding
This research is part of the project No. 2022/45/P/ST6/02969 co-funded by the National Science Centre and the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 945339.
Project
Deep Neural Networks are nowadays a dominant tool used in most applications of AI. They suffer from the inability to handle epistemic uncertainty, the requirement for large processed (e.g., labeled) datasets, and finally, the dependence on implicit inductive biases. The difficulties of classic deep learning approaches can be alleviated by taking the Bayesian perspective and incorporating Bayesian components into the modeling framework, which altogether gives rise to modern Bayesian deep learning. Despite great expectations from BNNs as an approach that bridges two very successful methodologies, namely Deep and Bayesian learning, results so far have been unsatisfactory. The theoretical superiority of this class of models has not yet been successfully confirmed by applications.
Some challenges are related to modeling and model specification. In particular, we lack intuition about priors, and it is unclear how they should be specified. For example, it is an open question how priors should depend on model structure or even what their role should be (in Bayesian learning, priors can not only carry some kind of upfront information about the data, but for example, shrinkage or clustering priors can also bias learning towards certain outcomes).
Another challenging aspect is learning. Existing inference methods are unable to recover posteriors for models with hundreds of parameters, even with multiple simplifications. Additionally, the learning limitations reflect on modeling capabilities. For example, by assuming a Gaussian posterior with a diagonal covariance matrix learned using variational inference, we may also implicitly filter out some potential impacts or benefits of priors.
Better uncertainty quantification, OOD detection, and model calibration are possible by addressing the above challenges jointly and accounting for priors, model structure, and learning methods at the same time.
Main Hypothesis
Priors, architecture and learning method decided together lead to better performance.
Research Questions
- RQ1: How better priors can improve performance of BNNs?
- RQ2: What architectures of priors and posteriors are optimal?
- RQ3: How to select priors for BNNs?
- RQ4: Shall models with advanced priors be handled in a more or less Bayesian way?
Preceding publications
T. Kuśmierczyk, J. Sakaya, A. Klami: Correcting Predictions for Approximate Bayesian Inference. AAAI 2020.
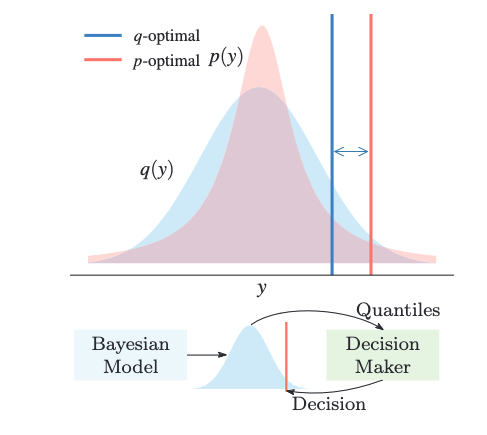
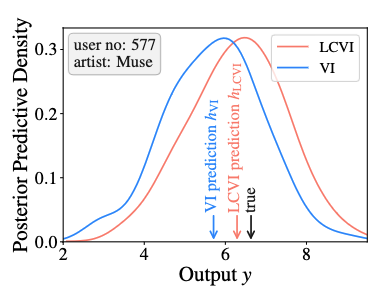
Bayesian models quantify uncertainty and facilitate optimal decision-making in downstream applications. For most models, however, practitioners are forced to use approximate inference techniques that lead to sub-optimal decisions due to incorrect posterior predictive distributions. We present a novel approach that corrects for inaccuracies in posterior inference by altering the decision-making process. We train a separate model to make optimal decisions under the approximate posterior, combining interpretable Bayesian modeling with optimization of direct predictive accuracy in a principled fashion. The solution is generally applicable as a plug-in module for predictive decision-making for arbitrary probabilistic programs, irrespective of the posterior inference strategy. We demonstrate the approach empirically in several problems, confirming its potential.
T. Kuśmierczyk, J. Sakaya, A. Klami: Variational Bayesian Decision-making for Continuous Utilities. NeurIPS 2019.
Bayesian decision theory outlines a rigorous framework for making optimal decisions based on maximizing expected utility over a model posterior. However, practitioners often do not have access to the full posterior and resort to approximate inference strategies. In such cases, taking the eventual decision-making task into account while performing the inference allows for calibrating the posterior approximation to maximize the utility. We present an automatic pipeline that co-opts continuous utilities into variational inference algorithms to account for decision-making. We provide practical strategies for approximating and maximizing the gain, and empirically demonstrate consistent improvement when calibrating approximations for specific utilities.
